Predmet:Re: Skupovi
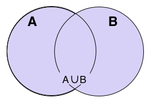
Skupovi se mogu sabirati. UNIJA skupova A i B je skup svih elemenata skupa A i skupa B.
A U B = B U A
A U A = A
A U ø =A
Skup koji nema ni jednog elementa zove se PRAZAN SKUP.
primjer
Skup svih realnih rjesenja jednacine x
2=-1 je prazan skup. Jednacina x
2=-1 nema rjesenja u skupu R
Skup zajednickih tacaka paralelnih pravi je prazan skup.
Skup svih ljudi visokih 4 m je prazan skup.
Prazan skup oznacavamo sa ø.

PRESJEK( zajednicki dio 2 skupa) je skup koji cine svi elementi koji su u skupu A i u skupu B. Oznacavamo ga sa A∩B ( citamo A presjek B).
A∩B ={x \ x iz A i x iz B}
Ako skupovi A i B nemaju zajednickih elemenata onda je presjek prazan skup.
Primjer
A={ 1, 2, 3}
B={0, 3}
A∩B ={3}
Za B={0, 4} : A∩B bi bio prazan skup. U tom slucaju skupovi A i B nemaju zajednickih elemenata.
Za dva skupa kazemo da su DISJUNKTNI ako nemaju zajednickih elemenata. njihov presjek je prazan skup. primjer su paralelni pravci (Euklidova geometrija)
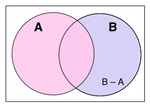
Skupovi se mogu oduzimati. KOMPLEMENT slupa A u odnosu na skup B (jos se koristi i naziv razlika skupova AiB) oznacavamo sa B − A, (ili B \ A), je skup svih elemenata koji su clanovi skupa B, ali nisu clanovi skupa A.
Potrebno je uociti da je valjana operacija "oduzimanja" clanova koji nisu u skupu, po poput micanja elementa zelena iz skupa {1,2,3} - takva operacija nema smisla.
{1,2}-{zelena}={1,2}
Ako oduzmemo skup A od samog sebe dobicemo prazan skup.
U odredjenim postavkama, svi skupovi koji se posmatraju, smatraju se podskupovima nekog datog univerzalnog skupa U. U takvim slucajevima, U − A zove se apsolutni komplement ili jednostavno komplement skupa A, i oznacava s A′, A
C .
Primjeri:
* {1, 2} − {crvena, bijela} = {1, 2}
* {1, 2, zelena} − {crvena, bijela, zelena} = {1, 2}
* {1, 2} − {1, 2} = ø
* Ako je U skup svih cijelih brojeva, P skup parnih brojeva, a N skup svih neparnih brojeva, tada komplement skupa P u U iznosi N, ili ekvivalentno, P′ = N.
"Ne treba se stidjeti nikakvog posla, pa čak ni onog najprljavijeg; treba se stidjeti samo besposlenog života." - Tolstoj