Centar za edukaciju-BiH

Predmet:Re: Zanimljive krive

---

Povrsina ogranicena jednim lukom cikloide i osom Ox je 3a²π

---

Predmet:Re: Zanimljive krive

---

PS:

---

Predmet:Re: Zanimljive krive

---

Zapremina tijela nastalog rotacijom jednog luka cikloide oko ose Ox je 5a³π²
gdje je a poluprecnik kruga.

---

Predmet:Re: Zanimljive krive

---

Hipocikloidu opisuje tacka na kruznici koja se, bez trenja kotrlja sa unutrasnje strane druge kruznice.



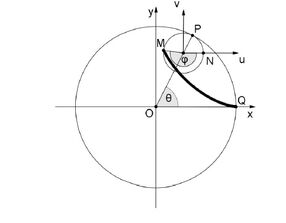
Pretpostavimo da se po unutrasnjosti kruznice K₀ poluprecnika a kotrlja bez trenja kruznica K poluprecnika b, b < a.

Neka je koordinatni pocetak u centru kruţnice K₀. Kruznicu K cemo postaviti tako da dodiruje kruznicu K₀ sa unutrasnje strane u tacki Q presjeka sa x osom. Posmatrajmo putanju koju opisuje tacka Q kada se kruznica K ravnomjerno kotrlja u smjeru suprotnom kretanju kazaljke na satu. Pretpostavimo da je Q poslije vremena t ta tacka presla u tacku M(x,y). Uslov da je kotrljanje bez trenja, znaci da je duzina aθ luka kruznice K jednaka duzini luka kruznice K₀.



Ako se kruznica K ravnomjerno kotrlja onda je predjeni put proporcionalan vremenu t. Tj.



pri cemu je k brzina kotrljanja.

Dakle, ako uzmemo da se kruznica K kotrlja za a duznih jedinica u jedinici vremena dobijamo



pa se ugao θ moze tretirati kao vrijeme.

Odredimo sada koordinate tacke M u koordinatnom sistemu xy. Koordinate centra kruznice na kojoj se nalazi tacka M su:

[img]http://img3.wikia.nocookie.net/...b53ab1.png [/img]

Postavimo koordinatni sistem uv tako da mu koordinatni pocetak bude u centru te kruznice K, a koordinatne ose paralelne sa x odnosno sa y osom. U tom koordinatnom sistemu koordinate u i v tačke M su :





Iz



dobijamo





Neka je a:b cio broj, odnosno a:b=s, mozemo pricati o duzini luka i povrsini hipocikloide.

Duzina luka hipocikloide je duzina svodova , tj duzina krive koju opise posmatrana tacka dok ne stigne do pocetnog polozaja.

Povrsina hipocikloide je povrsina koja je ogranicena sa uzastopnim svodovima hipocikloide

---

Predmet:Re: Zanimljive krive

---

Duzina luka hipocikloide je 8b(s-1), gde je b poluprecnik kruga koji se krece po unutrasnjosti nepokretnog kruga poluprečnika a i s=a:b je broj svodova hipocikloide.

Duzina luka krive je

















Na osnovu ovoga dobijamo da je duzina luka jednog svoda hipocikloide:

---

Predmet:Re: Zanimljive krive

---

Povrsina hipocikloide je

π b² (s-1)(s-2)

gdje je b poluprecnik kruga koji se krece po unutrasnjosti stalnog kruga poluprecnika a i s= a:b je broj svodova hipocikloide.

Koristicemo Grinovu teoremu
















Iz s=a:b proizlazi

---

Predmet:Re: Zanimljive krive

---

U slucaju kada je a=2b; s=2


jednacine hipocikloide (dijametra) su

x=2bcosθ

y=0

Tacka na kotrljajucem krugu osciluje po precniku kruznice. Ovo je jedan od najlepsih modela koje pokazuje kako pretvoriti kruzno kretanje u pravolinijsko i obrnuto. Duzina luka te hipocikloide je 8b

---

Predmet:Re: Zanimljive krive

---

Za a=3b; s=3 dobijamo trouglastu hipocikloidu (deltoidu, Stajnerovu krivu)



Njene jednacine su

x=2bcosθ + bcos2θ

y=2b sinθ - b sin2θ



Deltoida ima zanimljivo osobinu da odsjecci njenih tangenti unutar krive imaju konstantnu duzinu tj. jedan dio te duzine bi se mogao rotirati unutar nje stalno je dodirujuci.

Deltoida ima povrsinu P=2 π b²

Duzina lula je L=16b

---

Predmet:Re: Zanimljive krive

---

Za a=4b; s=4 dobijamo astroidu, sa parametarskim jednacinama:

x=3bcosθ + bcos3θ=acos³θ

y=3b sinθ - b sin3θ= asin³θ



Porijeeklo imena astroida moţe se naci u grckoj rijeci (asteri) cije je znacenje zvijezda. Ova kriva je ranije nazivana i kubocikloidom i paraciklom.



ma slicnu osobinu kao deltoida: ako se odsjecak fiksirane duzine krece u ravni tako da njegovi krajevi klize po koordinatnim osama, obvojnica dobijene familije odsjecaka je astroida

Povrsina astroide je P= 6 π b²

Duzina luka je L=24 b.

---

Predmet:Re: Zanimljive krive

---

a a=17; b=5; s=17/5 dobijamo hipocikloidu



Mali krug poluprecnika b pet puta treba da obidje veliki krug poluprecnika a da bi fiksna tacka došla u pocetni polozaj, tj da bi hipocikloida bila zatvorena.

Za a =π; b=1 ; s=π.
Kako je odnos precnika iracionalan, hipocikloida se nikada nece zatvoriti. Ako bi nastavili kotrljati
krug do beskonacnosti, dobili bi jedan prsten.



poslije 50 krugova

---